Q5. Does it matter whether the utility integral is written as
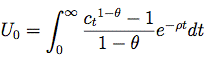 or
or Questions and answers of relevance for the
exam June 4, 2014
Course: Economic Growth
General remark: From what I write below nothing can be inferred about the particular contents of the exam assignments. My answers are written from the perspective of the matter in principle.
Questions received and my answers
Q1. What is most relevant, to redo the class exercises or the problems and answers from earlier exams?
Reply: Equally relevant, but considering earlier exam problems, those since 2011 are more relevant than those from 2010 or earlier. Before 2011 another textbook was used.
Q2. What is meant by saying "ignoring indivisibilities"?
Reply: An "divisibility" N(t) is a discrete variable "ignoring indivisibilities".
Q3. In connection with differential equations, what solution formulas are we supposed to recall and thereby be able to use without a hint?
Reply: Consider the appendix to Lecture Notes, Chapter 3. You should recall the trivial formula (*) at page 54 and the two last solution formulas associated with differential equation 3 at page 55, that is, the two solution formulas for the case b(t) = 0.
Q4. I think there is a typo in LN 9, page 141, line 9: "indeed integrating (9.9)" in my opinion should be "indeed integrating (9.14)". I hope not to be wrong.
Reply:
You are right. Thank you.
Q5. Does it matter whether the utility integral is
written as
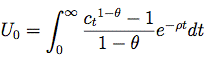 or
or ![]() ?
?
Reply:
No, the economic meaning of the two expressions is the same. This is because we
are always allowed to add or subtract a constant from a utility function. It
will still represent the same preferences. The marginal rate of substitution is
not affected and so the economic behavior is not affected.
It is thus just a matter of taste whether you write it one way or the other.
Some people prefer the first formula because it leads to a nice graph of
the family of CRRA utility functions for all theta > 0, including
theta = 1 (which has the interpretation u(c) = lnc). Other people prefer
the latter formula because it saves notation and avoids the inconvenience that
the utility integral with infinite horizon becomes unbounded for the sole reason
that an economically irrelevant constant, -1/(1-theta), has been added to the
instantaneous utility function.